香港科技大学、湘潭大学和南方科技大学的研究人员最近揭示了突变理论与非厄米物理学之间的可能联系，突变理论是一个专注于模拟突然变化(即突变)的数学领域。他们发表在《自然物理学》上的论文具体表明，一种结构丰富的简并，称为燕尾突变，可以自然存在于非厄米系统中。

“我们的工作受到之前利用同伦理论对拓扑奇点进行分类的研究的启发，这种技术已被用于研究液晶中的缺陷，例如向错和位错，”进行这项研究的研究人员之一贾宏伟说。Phys.org。“同伦理论也已应用于能带理论以研究非阿贝尔能带拓扑。在这些先前工作的基础上，我们试图扩展该方法以理解非厄米特系统中的奇点(表现为退化，称为异常点)。”

从本质上讲，Jia、Chan和他们的同事着手将特征向量坐标系沿环绕奇点(即函数“跳跃”或“坍缩”的点)的环路旋转的概念应用于非厄米系统。虽然在最近关于厄米特系统的其他研究中，特征向量是实数且正交，形成欧几里得空间的正交基，但将此特征向量框架旋转应用于非厄米特系统提出了一系列挑战。

“在这些非Hermitian系统中，特征向量不是正交的，因为特征向量的正交关系由Minkowski型不定内积定义。因此，沿着闭合路径，特征向量框架不仅旋转而且变形。特别是，当路径遇到异常表面时，特征向量会合并，”Jia解释道。

“这带来了一个严重的问题，因为传统的同伦环永远不会穿过退化。但这在我们的例子中是无法避免的，因为所考虑的退化线完全嵌入在特殊的表面上。在解决这些数学上具有挑战性的困难时，我们寻求数学家的帮助YifeiZhu。物理学家和数学家之间的这种合作导致了对非厄尔米特系统中奇点的拓扑特性的新见解。”

与Zhu、Jia、Chan和他们的同事合作，着手探索非厄米系统中退化(称为异常曲面、孤立和非孤立奇点)的发生，以及这些退化对对称性的依赖性。为实现这一目标，他们在参数空间中的特定对称性下追踪哈密顿矩阵的特征多项式的判别式中的零点。

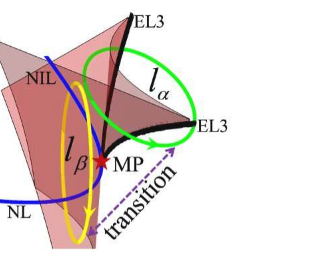
“我们使用数学软件、纸模型和3D打印等各种工具进行了许多数学实验，”贾说。“通过分析具有特定对称性的哈密顿量的显式示例，我们发现这种奇点特征的出现在具有我们选择的对称性的非厄米系统中是普遍的。我们还证明了在异常表面，异常表面横向相交的无缺陷交叉线(NIL)，以及与异常表面隔离的节点线(NL)。”

贾和他的同事进行的实验和计算产生了几个有趣的发现。首先，该团队发现，他们观察到的明显简并线始终可以在单个交汇点稳定连接，并且这种独特的结构受到对称性保护。

在这个图中，我们可以发现它是四个燕尾的组合结构。可以形成这样一个有趣的结构，因为环绕两条节点线(NL)的环路在拓扑上等同于环绕四条异常三阶线(EL3)的环路。目前无法证明这一点，需要更强大的数学工具来完成这项任务。学分：胡等人

“我们观察到异常表面以燕尾形相交，这让人想起数学和突变理论(特别是ADE分类)中的燕尾灾难，”贾说。“然而，我们的案例与ADE分类中的燕尾灾难之间存在显着差异，因为后者是通过检查四次多项式的多个根的轨迹来描述的，而我们的案例则来自我们正在研究的对称性，它编码了特征向量演化的信息。“

这组研究人员最近的工作在数学突变理论和非厄米物理学之间建立了联系，这两个研究领域以前被认为是不相关的。该团队使用同伦方法，试图获得对非厄米系统中非孤立奇点的拓扑理解。

贾和他的同事们最终揭示了在他们观察到的灾难的燕尾结构中发生的几个有趣的新转变。值得注意的是，这些反直觉的过渡现象以先前研究尚未发现的方式受到保护。

“这项工作是我与物理学家CheTingChan和数学家YifeiZhu合作的结果，”贾说。“易飞引入交同伦理论对于解决这个问题至关重要。我们将我们的特征框架变形和旋转理论与交同伦相结合，成功地证明了燕尾中有趣的过渡现象是拓扑保护的。我们相信可能有是在这些平台中发现的其他有趣的物理现象。我们的互补知识将使我们能够进一步探索这个未知的研究领域。”

贾和他的同事在非厄尔米特带中观察到的燕尾灾难是一种全新的拓扑无间隙相。对该阶段的进一步检查可能会揭示新的物理现象和影响。研究人员现在正在进行针对两个有趣现象的研究，第一个是这种新型无间隙相中的体积-边缘对应。

“我们正在探索燕尾结构中固有的无间隙相是否也可以支持拓扑边缘状态，”贾说。“我们正在探索的第二个现象是非常规的体费米弧，它在成对的尖点处连接了一对特殊的三阶线。”

除了为未来的物理研究提供信息外，这组研究人员收集的发现还可能导致数学领域的新研究。贾和他的同事们觉得他们工作中的数学部分仍然是临时的和不完整的，他们计划在下一个工作中进一步发展它。

“理论上，尽管研究对象已经可以用纯数学方式(在ADE分类中)进行表述，但这种表述仅给出了表面上可比较的结构，而潜在的特征与当前情况有很大不同，”贾解释说。“例如，ADE分类中燕尾的交汇点是一个特殊的四阶点，但当前燕尾的交汇点是提供两个线性独立本征态的三重简并。

“在冰山一角下掌握数学上系统的、物理上有意义的和实验上可实现的结构将是一个真正的挑战和机会。我们还认为代数方法、交同伦/同源性应该得到进一步发展，因为它是理解物理和数学中此类非孤立奇点的有力工具。”

版权说明：本站所有作品图文均由用户自行上传分享，仅供网友学习交流。若您的权利被侵害，请联系我们

标签：研究数学系统