1993年6月23日，数学家安德鲁·怀尔斯(AndrewWiles)做了三场讲座中的最后一场，详细介绍了他对费马大定理的解决方案，该定理是一个三个半世纪以来仍未解决的问题。怀尔斯的宣布在数学界和媒体上引起了轰动。

除了为长期存在的问题提供令人满意的解决方案之外，怀尔斯的工作还标志着在两个重要但看似截然不同的数学领域之间建立桥梁的重要时刻。

历史表明，数学领域许多最伟大的突破都涉及在该学科看似不同的分支之间建立联系。这些桥梁让数学家，就像我们两个一样，将问题从一个分支转移到另一个分支，并获得新的工具、技术和见解。

费马大定理是什么?

费马最后定理与毕达哥拉斯定理类似，该定理指出任何直角三角形的边都给出方程x2+y2=z2的解。

每个不同大小的三角形都会给出不同的解，事实上，有无数个解，其中x、y和z三个都是整数，最小的例子是x=3、y=4和z=5。

费马的最后一个定理是关于如果指数变为大于2时会发生什么。x3+y3=z3是否存在整数解?如果指数是10、50、3000万呢?或者，最常见的是，任何大于2的正数又如何呢?

1637年左右，皮埃尔·德·费马(PierredeFermat)声称答案是否定的，对于任何大于2的n，不存​​在三个正整数可以解xn+yn=zn。这位法国数学家将此断言写在他在一本古希腊数学教科书的页边空白处宣称，他有一个奇妙的证据，证明页边空白“太窄而无法容纳”。

费马所谓的证明从未被发现，而他的儿子死后发表的他的“最后定理”继续困扰着数学家几个世纪。

寻找解决方案

在接下来的356年里，没有人能找到费马丢失的证明，但也没有人能证明他错了——甚至荷马·辛普森也不能。该定理很快就因其难以证明甚至不可能证明而闻名，并提出了数千个错误的证明。该定理甚至被载入吉尼斯世界纪录，被称为“最难的数学问题”。

这并不是说没有任何进展。费马本人已经在n=3和n=4的情况下证明了这一点。许多其他数学家，包括先驱者索菲·杰曼(SophieGermain)，在费马方法的启发下，为n的个体值提供了证明。

但是，对于数学家来说，知道费马大定理对于某些数字成立还不够，我们需要知道它对于无穷多个数字都成立。数学家想要一个能同时适用于所有大于2的数字的证明，但几个世纪以来似乎找不到这样的证明。

然而，到了20世纪末，越来越多的研究表明费马大定理应该是正确的。这项工作的核心是模块化猜想，也称为谷山志村猜想。

两个世界之间的桥梁

模块化猜想提出了两个看似无关的数学对象之间的联系：椭圆曲线和模块化形式。

模块化形式的对称性可以从它如何变换圆盘中看出。图片来源：LinasVepstas，CCBY-SA3.0，来自WikimediaCommons

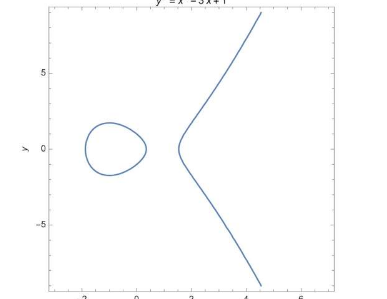
椭圆曲线既不是椭圆也不是曲线。它们是三次方程解的环形空间，例如y2=x3—3x+1。

模形式是一种函数，它接受某些复数(由实部和虚部两部分组成的数字)并输出另一个复数。这些函数的特殊之处在于它们高度对称，这意味着它们的外观有很多条件。

没有理由期望这两个概念是相关的，但这就是模块化猜想所暗示的。

最后来一个证明

模块化猜想似乎没有提及像xn+yn=zn这样的方程。但20世纪80年代数学家的工作表明了这些新思想与费马旧定理之间的联系。

首先，在1985年，格哈德·弗雷(GerhardFrey)意识到，如果费马错了，并且对于某个大于2的n，可能存在xn+yn=zn的解，该解将产生奇特的椭圆曲线。然后肯尼思·里贝(KennethRibet)在1986年证明，在模块化猜想也成立的宇宙中，这样的曲线不可能存在。

他们的工作意味着，如果数学家能够证明模性猜想，那么费马的最后一个定理必定是正确的。对于包括安德鲁·威尔斯(AndrewWiles)在内的许多数学家来说，研究模性猜想成为证明费马大定理的一条途径。

怀尔斯工作了七年，大部分时间都是秘密进行的，试图证明这个困难的猜想。到1993年，他即将证明模块化猜想的一个特例——这就是他证明费马大定理所需的一切。

安德鲁·怀尔斯(AndrewWiles)因其在费马大定理方面的研究而于2016年荣获阿贝尔奖，这是数学界的一项崇高荣誉。

1993年6月，他在艾萨克·牛顿研究所的一系列讲座中展示了他的工作。尽管随后的同行评审发现怀尔斯的证明存在缺陷，但怀尔斯和他以前的学生理查德·泰勒又花了一年的时间来填补这一空白并巩固了费马的最后一个证明。定理作为数学真理。

持久的后果

费马最后定理及其解决方案的影响继续在数学世界中产生影响。2001年，包括泰勒在内的一组研究人员在怀尔斯工作的启发下，在一系列论文中全面证明了模块化猜想。椭圆曲线和模形式之间的这座完整的桥梁已经并将继续成为理解数学的基础，甚至超越费马最后定理。

怀尔斯的工作被认为开启了“数论的新时代”，并且是现代数学重要部分的核心，包括广泛使用的加密技术和被称为“朗兰兹计划”的巨大研究工作，该计划旨在在两个基本原理之间架起一座桥梁。数学领域：代数数论和调和分析。

尽管怀尔斯主要是孤立地工作，但他最终需要同行的帮助来识别并填补他最初证明中的空白。如今，数学越来越成为一种协作性的努力，完成模块化猜想的证明所需要的努力就证明了这一点。这些问题庞大而复杂，通常需要多种专业知识。

那么，最后，费马真的像他声称的那样证明了他的最后一个定理吗?就数学家现在所知的情况而言，我们今天的许多人都不相信他做到了。尽管费马很聪明，但他有时也会犯错。数学家可以接受他相信自己有证明，但他的证明不太可能经得起现代检验。

版权说明：本站所有作品图文均由用户自行上传分享，仅供网友学习交流。若您的权利被侵害，请联系我们

标签：定理数学费马