最近，包括切里顿计算机科学学院教授克雷格·卡普兰博士在内的一个四人国际团队发现了一种单一形状，可以以一种永远无法重复的模式平铺平面(无限的二维表面)。

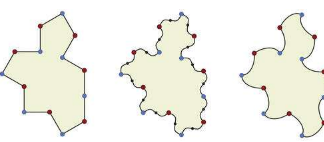
这一发现让数学家、瓷砖爱好者和公众着迷。

这种形状是一个13边形的多边形，他们称之为“帽子”，数学家将其称为非周期单瓦或“爱因斯坦”，德语中的意思是“一块石头”。

但该团队的最新发现再次提高了标准。他们发现了另一种与第一种形状相关的形状，它符合更严格的定义。这种新形状被称为“幽灵”，它以一种图案平铺一个平面，如果不使用该形状的镜像，这种图案就不会重复。因此，它也被称为“吸血鬼爱因斯坦”——一种非周期性平铺而不需要反射的形状。

卡普兰解释说：“我们的第一篇论文解决了爱因斯坦问题，但由于形状需要反射才能不定期地平铺，人们提出了一个合理的问题：是否有一种形状可以完成帽子的功能，但不需要反射。”“我们很幸运，我们找到了一种形状，不仅可以解决这个子问题，而且在第一篇论文发表后很快就解决了它。”

对于数学家来说，帽子及其镜像是单一形状，但在物理世界中，左手和右手形状可以表现不同。例如，您不能将右手手套戴在左手上。

卡普兰说：“如果你不定期地在一个大浴室地板上铺上一侧上釉的帽子形状的瓷砖，那么你就需要帽子和帽子的镜像。”

但促成最近发现的并不是这个狡辩。

吸血鬼爱因斯坦的发现始于大卫史密斯的沉思，他是一位来自英国约克郡的退休印刷技术员和自称形状爱好者，几个月前他的好奇心导致了最初的爱因斯坦发现。

卡普兰说：“我们的帽子纸上线几天后，戴夫给我们发了一封电子邮件，说他一直在摆弄一个看起来表现得很奇怪的相关形状。”“日本数学家和著名艺术家YoshiakiAraki的作品秉承了MCEscher的精神，他发布了Tile(1,1)的图片，这让Dave有兴趣进一步研究它。”

Yoshiaki在Twitter上发布了一个有趣的问题：“基于新的非周期单块Tile(1,1.1)的非周期海龟镶嵌。在平铺中，据说大约12.7%的瓷砖被反射。绿色的就是一个例子。再一个倒影的乌龟藏在瓷砖里。倒影的是谁?'”

“Yoshi将Tile(1,1)变成了海龟，在图片中看到另一只反射的海龟有点困难。但这让Dave很好奇。如果我们用这种形状平铺但没有反射会怎么样?当他这样做时，Dave发现他可以以一种不会停止、不会重复的模式逐渐向外建造瓷砖。”

但随后这个形状却带来了不同的争议。正如Kaplan所解释的，如果您使用Tile(1,1)的反射，该图案确实会重复。换句话说，它是周期性的。但是，如果通过用曲线替换其直边来修改Tile(1,1)，它就会变成吸血鬼爱因斯坦——一种没有反射的单一形状，以永远无法重复的图案平铺无限平面。

对于数学家和瓷砖爱好者来说，显而易见的问题是接下来会发生什么?

“我们可以提出问题的许多变体，”卡普兰说。“至少对我来说，最有趣的是这是否可以在3D中完成。如果有一个在三维空间中非周期性重复的形状，那就太好了。这样的结构更难可视化，但从计算角度来看，它并没有那么难。更难证明的是，如果我们幸运地找到一种三维形状(一种多形体)，它只是不定期地像帽子瓷砖一样。”

“平铺理论作为数学的一个分支是美丽的、有形的，并且有很多令人着迷的问题需要解决。不乏后续工作要做。”

Hatfest是为了庆祝“帽子”的发现而举办的，将于7月20日至21日在牛津大学数学研究所举行。该活动的第一天将针对非专业观众举办关于瓷砖的演讲和研讨会，而第二天将以针对广大物理学家和数学家观众的演讲为特色。

版权说明：本站所有作品图文均由用户自行上传分享，仅供网友学习交流。若您的权利被侵害，请联系我们

标签：形状帽子瓷砖