众所周知，正态分布是概率和统计学中的一个重要工具。它可以被描述为一种服从普遍规则的分布，该规则源自概率中最重要的定理之一：中心极限定理，通常称为 CLT。更实际地讲，它还描述了一些数据如何自然地聚集在一个中心值周围，其相应直方图(表示数据的分布)的形状是均衡的钟形曲线。

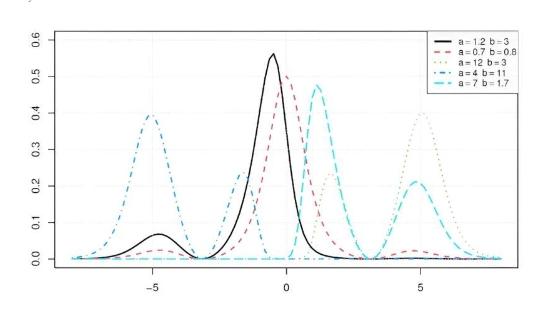
一些来自现实世界过程的数据遵循这种模式，因此正态分布是分析这些数据的一个选项。然而，对于大多数数据来说，理想的钟形形状是出乎意料的。事实上，有时数据是倾斜的，这意味着相关的直方图向左或向右倾斜。在其他情况下，数据可能有多个模式(峰值)而不是一个中心值。这些变化使得正态分布在分析此类数据集时不太准确。

数学理论有助于解决这些问题。通过引入对偏度和峰度的调整，我们可以修改正态分布的形状可能性。另一方面，转换技术可以处理多种模式，从而提供更灵活的方法。本质上，数学理论提供了扩展正态分布的必要工具，使其更适用于不同类型的数据。这提高了模型和预测的准确性，从而提高了决策的准确性。

目前已有多种策略，但很少有策略能够通过高度可调的配置同时扭曲和增加正态分布的模式。在《不对称》杂志上发表的论文《创建不对称连续分布的新数学解决方案》中开发了这种选项。

使用两个几乎不受约束的参数和一个非常通用的中间函数，奠定了新数学策略的理论基础和保证。该策略的关键在于这些组件的选择具有无限的可能性;中间函数可以选择为指数、对数、三角函数，以及各种函数类型。根据它们的性质，可以达到各种右偏、左偏和多峰形状。

这些形状中的每一种都可以对应于在现实世界数据分析中遇到的直方图形状。相关理论的另一个重要方面是，正态分布可以用具有相同支持的任何分布代替，从而使该策略能够适应许多现实世界场景。本文使用柯西分布从理论上说明了这一点。只需付出很少的努力，它也可以适应生存分布，从而开辟了远远超出基本正态分布性质的新视角。

目前正在利用来自生物、医学、工程和金融等不同领域的数据开发这一理论验证策略的实际应用。我们还在准备一个 R 包，以便任何处理非标准模式数据的人都可以使用它。

版权说明：本站所有作品图文均由用户自行上传分享，仅供网友学习交流。若您的权利被侵害，请联系我们

标签：