大数只能通过大量的计算工作才能分解。由WolfgangLechner领导的奥地利因斯布鲁克大学的物理学家现在正在为一种新型量子计算机提供蓝图，以解决因式分解问题，这是现代密码学的基石。该研究最近发表在《通信物理学》上。

今天的计算机基于执行所谓门的微处理器。例如，门可以是“与”运算，即，将两个位相加的运算。这些门以及计算机是不可逆的。也就是说，算法不能简单地向后运行。因斯布鲁克大学理论物理学教授WolfgangLechner解释说：“如果你乘法2x2=4，你不能简单地反向运行这个运算，因为4可能是2x2，但同样是1x4或4x1。”然而，如果这是可能的，那么对大数进行因式分解将是可行的，即将它们分成它们的因子。

来自因斯布鲁克大学理论物理学研究所的MartinLanthaler、BenNiehoff和WolfgangLechner以及量子衍生公司ParityQC现在已经在量子计算机的帮助下开发出这种算法的反转。起点是经典逻辑电路，它将两个数字相乘。如果输入两个整数作为输入值，电路将返回它们的乘积。这样的电路是由不可逆操作构建的。“然而，电路的逻辑可以在量子系统的基态中编码，”WolfgangLechner团队的MartinLanthaler解释说。“因此，乘法和因式分解都可以理解为基态问题，并使用量子优化方法来解决。”

所有可能结果的叠加

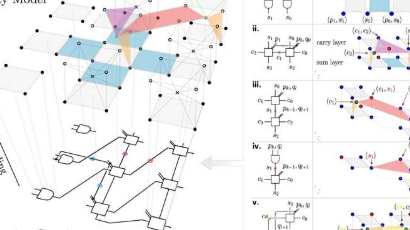
“我们工作的核心是对乘法器电路的基本构建块进行编码，特别是与门、具有奇偶校验架构的半加器和全加器作为相互作用自旋集合的基态问题，”MartinLanthaler说。

编码允许整个电路由重复的子系统构建，这些子系统可以排列在二维网格上。通过将这些子系统中的几个串联在一起，可以实现更大的问题实例。与测试所有可能因素的经典蛮力方法不同，量子方法可以加快搜索过程：要找到基态，从而解决优化问题，没有必要搜索整个能量景观，但更深入可以通过“隧道”到达山谷。

目前的研究工作为新型量子计算机解决分解问题提供了蓝图，分解问题是现代密码学的基石。该蓝图基于因斯布鲁克大学开发的奇偶校验架构，可在当前所有量子计算平台上实施。

版权说明：本站所有作品图文均由用户自行上传分享，仅供网友学习交流。若您的权利被侵害，请联系我们

标签：量子问题计算机